第1章 曲线和曲面的表示
本文最后更新于 2025年9月1日
Bézier曲线和曲面
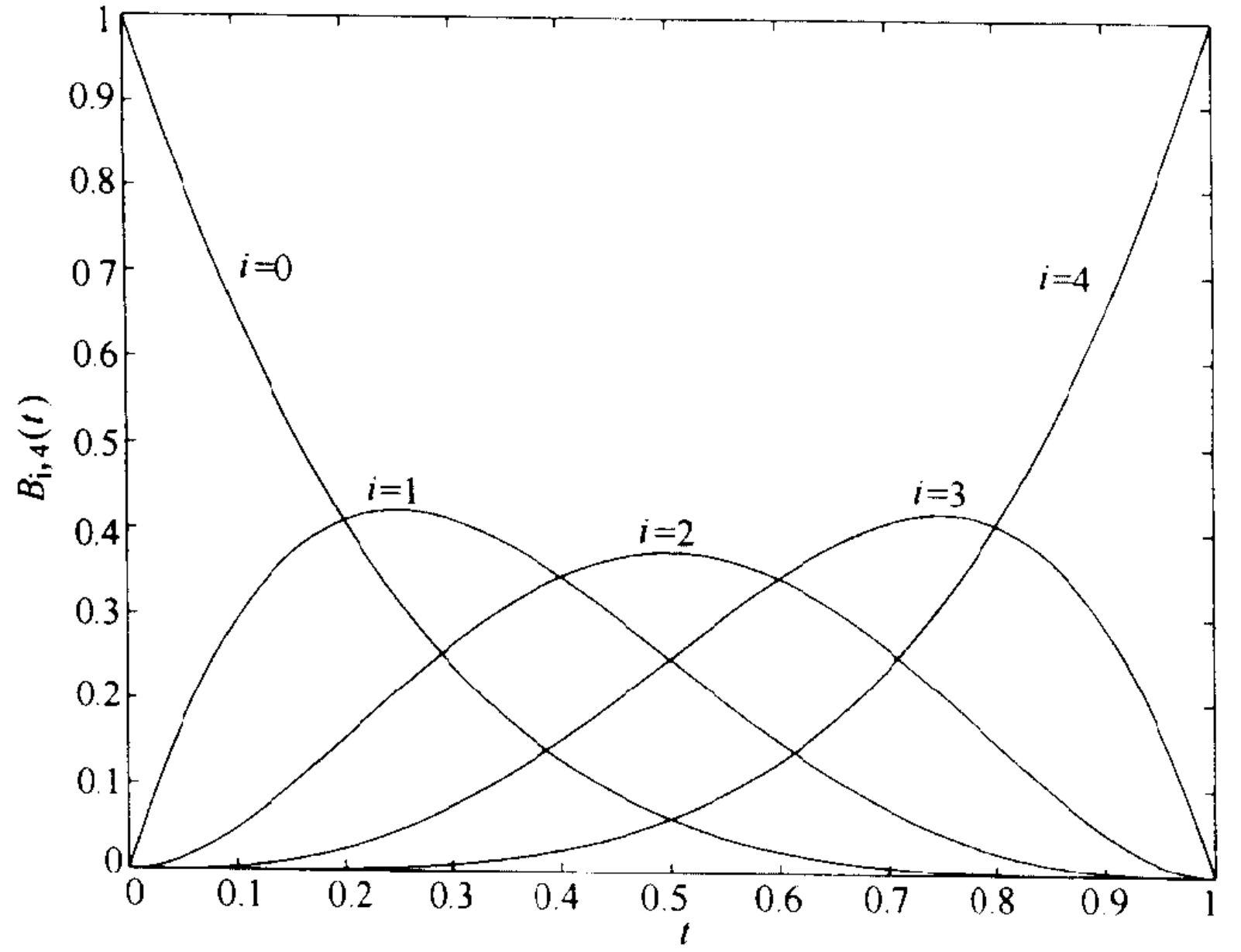
Bernstein多项式
定义:
$$
B_{i,n}(t)=\frac{n!}{i!(n-i)!}(1-t)^{n-i}t^i, \quad i=0,\cdots,n
$$
形成多项式空间的一组基。具有如下性质:
- 非负性:$B_{i,n}(t)\geq 0,\ 0\leq t\leq 1,\ i=0,\cdots,n$
- 单位分割性:由二项式定理可知,$\sum_{i=0}^n B_{i,n}(t)=1$
- 对称性:$B_{i,n}(t)=B_{n-i,n}(1-t)$
- 递归性:$B_{i,n}(t)=(1-t)B_{i,n-1}(t)+tB_{i-1,n-1}(t)$。规定:当$i<0$或$i>n$时,$B_{i,n}(t)=0$;$B_{0,0}(t)=1$。
- 线性精度:$t=\sum_{i=0}^n\frac{i}{n}B_{i,n}(t)$
- 升阶性质:$n$次基函数可以表示为$n+1$次或更高次基函数的线性组合。
$$
\begin{gather*}
B_{i,n}(t)=\left(1-\frac{i}{n+1}\right)B_{i,n+1}(t)+\frac{i+1}{n+1}B_{i+1,n+1}(t),\quad i=0,1,\cdots,n
\newline
B_{i,n}(t)=\sum_{j=i}^{i+r}\frac{\binom{n}{i}\binom{r}{j-i}}{\binom{n+r}{j}}B_{j,n+r}(t),\quad i=0,1,\cdots,n
\end{gather*}
$$
导数:
$$
\frac{\mathrm{d}B_{i,n}(t)}{\mathrm{d}t}=n\left[B_{i-1,n-1}(t)-B_{i,n-1}(t)\right]
$$
Bézier曲线的定义和性质
一条$n$次($n+1$阶)Bézier曲线可以表示为:
$$
\symbfit{r}(t)=\sum_{i=0}^n {\symbfit{b}}_iB_{i,n}(t),\quad 0\leq t\leq1
$$
系数$\symbfit{b}_i$称为控制顶点。顺序连接控制顶点得到的直线段形成曲线的控制多边形。
Bézier曲线具有如下性质:
- 几何不变性:平移和旋转控制顶点时,曲线形状不变
- 端点的几何性质:
- 首尾两个控制顶点就是曲线的两个端点,$\symbfit{b}_0=\symbfit{r}(0)$,$\symbfit{b}_n=\symbfit{r}(1)$。
- 在端点处,曲线与控制多边形相切。定义:$\Delta\symbfit{b}_i=\symbfit{b}_{i+1}-\symbfit{b}_i$。
$$
\dot{\symbfit{r}}(t)=n\sum_{i=0}^{n-1}\Delta\symbfit{b}_iB_{i,n-1}(t),\quad 0\leq t\leq1
$$
Bézier曲线的一阶导数称为速端曲线,也是一条Bézier曲线,次数比原曲线低一次,控制顶点为$n\Delta\symbfit{b}_i$。
- 凸包性质:Bézier曲线的凸包就是包含所有顶点的所有凸区域的交集边界。
- 变差缩减性质:一条直线与Bézier曲线交点个数不会多于该直线与控制多边形交点个数。
- 对称性质:如果将控制顶点重新编号为$\symbfit{b}_{n-i}^*=\symbfit{b}_i$,根据Bernstein多项式的对称性有:$\sum_{i=0}^n\symbfit{b}_iB_{i,n}(t)=\sum_{i=0}^n\symbfit{b}_i^*B_{i,n}(1-t)$。
Bézier曲线的算法
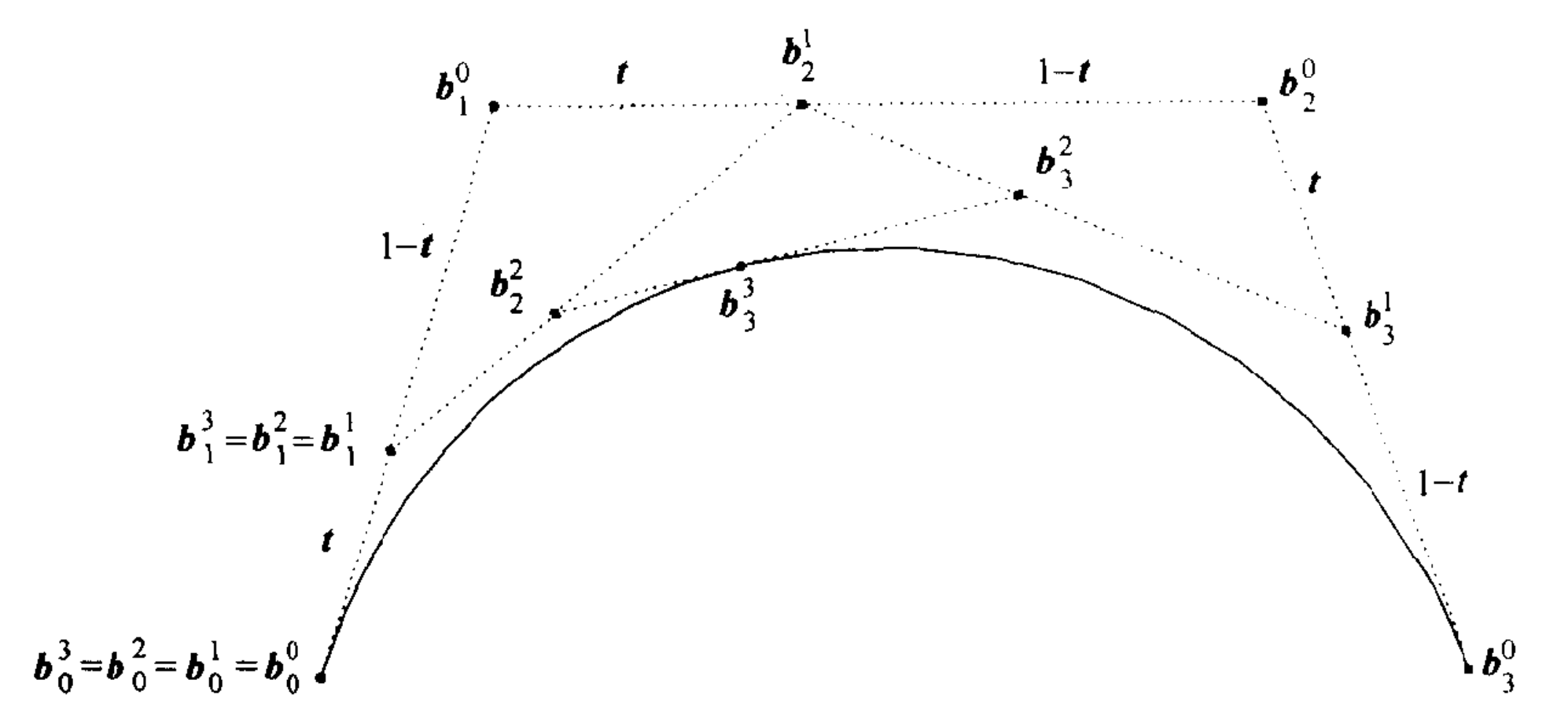
de Casteljau算法
用于求曲线在参数$t_0$处的值和在该参数处剖分曲线。
$$
\symbfit{b}_i^k(t_0)=(1-t_0)\symbfit{b}_{i-1}^{k-1}+t_0\symbfit{b}_i^{k-1},\quad k=1,2,\cdots,n,\quad i=k,\cdots,n
$$
递归应用可以求得新的控制顶点。算法具有如下性质:
- 点$\symbfit{b}_i^0$是曲线原始控制顶点;
- 曲线在参数$t_0$处的值是$\symbfit{b}_n^n$;
- 曲线在参数$t_0$处剖分成两段Bézier曲线,控制顶点分别为:${\symbfit{b}_0^0,\symbfit{b}_1^1,\cdots,\symbfit{b}_n^n}$和${\symbfit{b}_n^n,\symbfit{b}_n^{n-1},\cdots,\symbfit{b}_n^0}$。
连续性算法
两段Bézier曲线连接表示复杂曲线时需要考虑两条曲线之间的连续性。
- $G^0$连续:位置连续,要求两条曲线的端点重合。
- $G^1$连续:切向连续,要求相邻曲线在端点处具有相同的切向。
- $G^2$连续:曲率连续,要求曲率中心连续通过曲线间的连接点。
更为严格的连续性条件是参数连续条件: - $C^k$连续:要求曲线在连接点处直至$k$阶导数相等。
升阶算法
在保持曲线形状不变的前提下,将$n$次Bézier曲线提升为$n+1$次Bézier曲线,控制点数目加1。新的控制顶点根据$\symbfit{b}_i^{n+1}=\frac{i}{n+1}\symbfit{b}_{i-1}^n+\left(1-\frac{i}{n+1}\right)\symbfit{b}_i^n$计算。
Bézier曲面
$$
\symbfit{r}(u,v)=\sum_{i=0}^m\sum_{j=0}^n\symbfit{b}_{ij}B_{i,m}(u)B_{j,n}(v),\quad 0\leq u,v\leq1
$$
连接相邻控制顶点$\symbfit{b}_{ij}$的所有线段形成曲面的控制网。边界等参数线($u=0,u=1,v=0和v=1$)的控制顶点与控制网的边界点重合。
Bézier曲面继承了Bézier曲线的许多性质,如:几何不变性,端点几何性质,凸包性质,但不具有变差缩减性质。
B-样条曲线和曲面
B-样条
B-样条基函数$N_{i,k}(t)$定义如下。当$k=1$时,
$$
N_{i,1}(t)=\begin{cases}1,\quad &t_i\leq t<t_{i+1}\newline
0,\quad &t<t_i或t\geq t_{i+1}\end{cases}
$$
当$k>1$且$i=0,1,\cdots,n$时,
$$
N_{i,k}(t)=\frac{t-t_i}{t_{i+k-1}-t_i} N_{i,k-1}(t)+\frac{t_{i+k}-t}{t_{i+k}-t_{i+1}}N_{i+1,k-1}(t)
$$
上述方程具有下列性质:
- 正值性质:当$t_i<t<t_{i+1}$时,$N_{i,k}(t)>0$。
- 局部支撑性质:当$t_0\leq t\leq t_i$或$t_{i+k}\leq t\leq t_{n+k}$时,$N_{i,k}(t)=0$。
- 单位分割性质:$\sum_{i=00}^nN_{i,k}(t)=1,\ t\in [t_o,t_m]$。
- 递归性质。
- 连续性质:$N_{i,k}(t)$在单节点处是$C^{k-2}$连续的。
结点(nodes或Greville横坐标)定义为节点的平均值:
$$
\xi_i=\frac1{k-1}\left(t_{i+1}+t_{i+2}+\cdots+t_{i+k-1}\right)
$$
B-样条基函数的导数:
$$
\frac{\mathrm{d}N_{i,k}(t)}{\mathrm{d}t}=\frac{k-1}{t_{i+k-1}-t_i}N_{i,k-1}(t)-\frac{k-1}{t_{i+k}-t_{i+1}}N_{i+1,k-1}(t)
$$
B-样条曲线
B-样条曲线定义为控制顶点$\symbfit{p}_i$和B-样条基函数$N_{i,k}(t)$的线性组合:
$$
\symbfit{r}(t)=\sum_{i=0}^n \symbfit{p}_iN_{i,k}(t),\quad n\geq k-1,\ t\in[t_{k-1},t_{n+1}]
$$
基函数$N_{i,k}(t)$定义在节点向量$\symbfit{T}=(t_0,t_1,\cdots,t_{k-1},t_k,\cdots,t_n,t_{n+1},\cdots,t_{n+k})$上。具有$n+k+1$个节点,即控制顶点数目$n+1$加曲线阶数$k$。
B-样条曲线具有如下性质:
- 几何不变性。
- 端点几何性质:
- B-样条曲线通常不通过两端控制顶点。增加节点重数会降低曲线在该节点处的连续性,在$k-1$重节点处,控制多边形与曲线重合,在$k$重节点处,曲线不连续。端点插值型(clamped):将端节点重复$k$次可以使得曲线端点与控制多边形重合。如下图所示,有$t_0=t_1=\cdots=t_{k-1}=t_k$。
- 如上定义的节点向量确定的B-样条曲线在端点处与控制多边形相切。
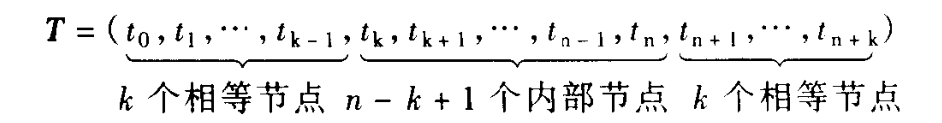
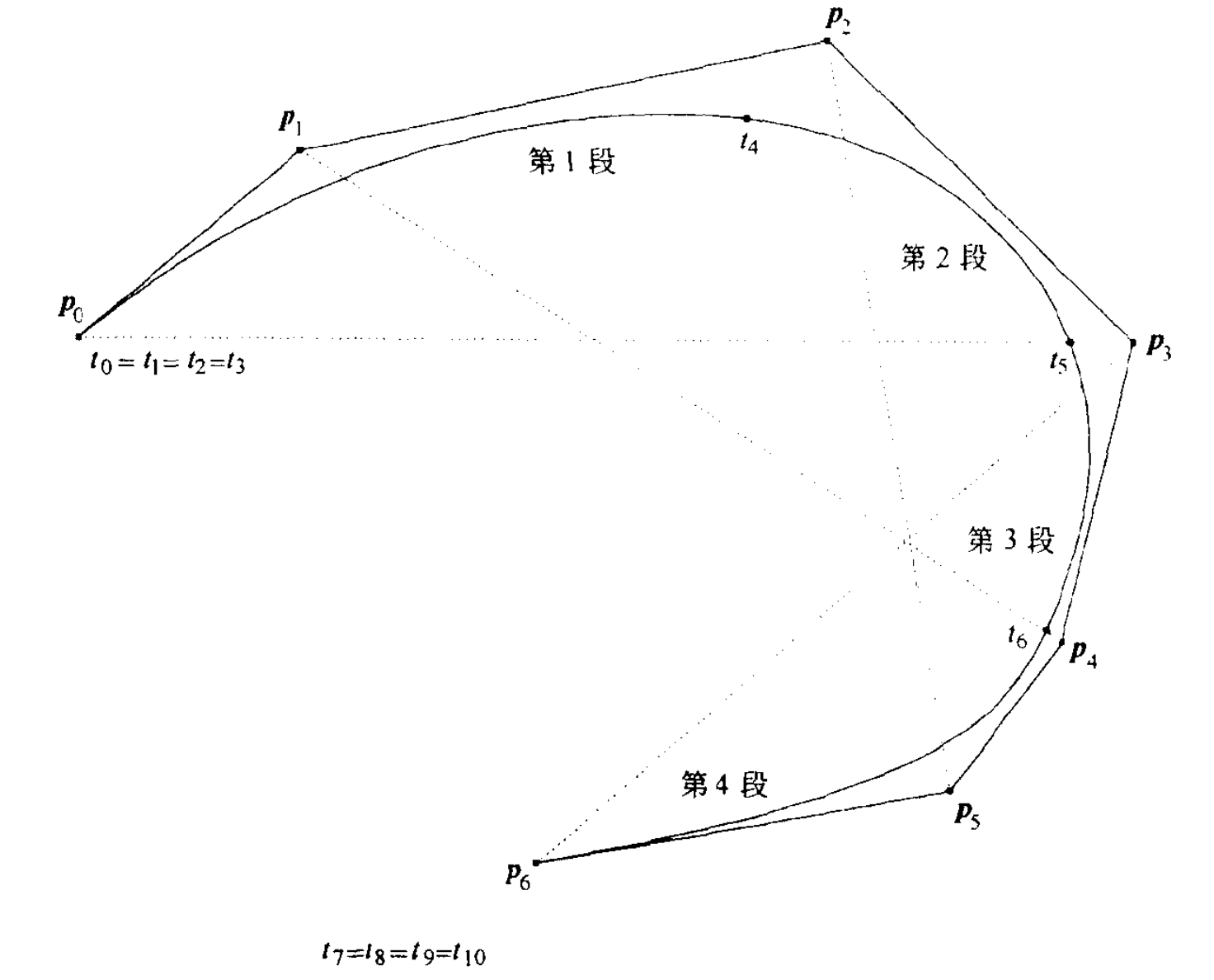
- 凸包性质:一段曲线位于影响它的控制顶点的凸包内。如上图中的三次B-样条曲线的第$i$段曲线位于由控制顶点$\symbfit{p}_{i-1},\symbfit{p}_i,\symbfit{p}_{i+1},\symbfit{p}_{i+2}$形成的凸包内。
- 局部支撑性质:B-样条曲线中的一段曲线是由$k$个控制顶点控制的,每一个控制顶点影响$k$段曲线。
- 变差缩减性质:一条直线与B-样条曲线的交点个数不多于该直线与控制多边形的交点个数。
- B-样条曲线转化为Bézier曲线的性质:$k$阶($k-1$次)Bézier曲线是一条特殊的B-样条曲线,节点向量没有内部节点,端节点是$k$重节点,节点向量为:
$$
\symbfit{T}=(t_0,t_1,\cdots,t_{k-1},t_{n+1},\cdots,t_{n+k}),\quad n=k-1且前/后k个节点分别相等
$$
B-样条曲线的算法
de Boor算法
用于在指定参数$\bar{t}$处求值和剖分,是de Casteljau算法的推广。
$$
\symbfit{r}(t)=\sum_{i=0}^{n+j}\symbfit{p}_i^jN_{i,k-j}(t),\quad j=0,1,\cdots,k-1
$$
其中
$$
\symbfit{p}_i^j=(1-\alpha_i^j)\symbfit{p}_{i-1}^{j-1}+\alpha_i^j\symbfit{p}_i^{j-1},\quad \alpha_i^j=\frac{\bar{t}-t_i}{t_{i+k-j}-t_i}且\symbfit{p}_j^0=\symbfit{p}_j
$$
Boehm算法
节点插入,新曲线与原曲线重合。
Tiller节点删除算法
B-样条曲面
具有矩形拓扑的控制顶点$\symbfit{P}_{ij}(0\leq i\leq m,0\leq j\leq n)$和两个节点向量$\symbfit{U}={u_0,u_1,\cdots,u_{m+k}}$和$\symbfit{V}={v_0,v_1,\cdots,v_{n+l}}$对应的整个B-样条曲面为:
$$
\symbfit{r}(u,v)=\sum_{i=0}^m\sum_{j=0}^{n}\symbfit{p}_{ij}N_{i,k}(u)N_{j,l}(v)
$$
$u=常数$或$v=常数$为B-样条曲面上的等参数线。$u=u_0$对应于曲面上$v$方向的一条参数线,节点向量为$\symbfit{V}$,控制顶点为$\symbfit{q}_j=\sum_{i=0}^m\symbfit{p}_{ij}N_{i,m}(u_0),\ (0\leq j\leq n)$。
B-样条曲面具有类似曲线的性质:几何不变、端点、凸包、转化为Bézier曲面的性质,但不具有变差缩减性质。
B-样条到NURBS的推广
非均匀有理B-样条(Non-Uniform Rational B-Spline, NURBS)具有和B-样条一样的性质,NURBS曲线表示为:
$$
\symbfit{r}(t)=\frac{\sum_{i=0}^n\omega_i\symbfit{p}_iN_{i,k}(t)}{\sum_{i=0}^n\omega_iN_{i,k}(t)}
$$
其中$\omega_i>0$为权因子,$N_{i,k}(t)$为B-样条基函数。如果所有权因子都是1,则NURBS退化为B-样条。如果控制顶点的个数等于NURBS曲线的阶数,那么曲线就简化为有理Bézier曲线:
$$
\symbfit{r}(t)=\frac{\sum_{i=0}^n\omega_i\symbfit{b}_iB_{i,n}(t)}{\sum_{i=0}^n\omega_iB_{i,n}(t)}
$$
NURBS曲线可以精确表示圆锥曲线。
NURBS曲面可以表示为:
$$
\symbfit{r}(u,v)=\frac{\sum_{i=0}^m\sum_{j=0}^n\omega_{ij}\symbfit{p}_{ij}N_{i,k}(u)N_{j,l}(v)}{\sum_{i=0}^m\sum_{j=0}^n\omega_{ij}N_{i,k}(u)N_{j,l}(v)}
$$
该公式可以精确表示二次曲面、圆环面、旋转面和一般的自由曲面。当所有的权因子为1时,NURBS就是B-样条曲面。如果沿参数$u$和$v$方向,控制顶点的个数均与B-样条基函数的阶一致,那么NURBS曲面可以转化为有理Bézier曲面:
$$
\symbfit{r}(u,v)=\frac{\sum_{i=0}^m\sum_{j=0}^n\omega_{ij}\symbfit{b}_{ij}B_{i,m}(u)N_{j,n}(v)}{\sum_{i=0}^m\sum_{j=0}^n\omega_{ij}B_{i,m}(u)B_{j,n}(v)}
$$