第2章 曲线的微分几何

弧长和切向量

定义曲线段$\symbfit{r}=\symbfit{r}(t)$，弧长微分：$\mathrm{d}s=|\dot{\symbfit{r}}|\mathrm{d}t$。
切向量：$\frac{\mathrm{d}\symbfit{r}}{\mathrm{d}t}$；单位切向量：$\symbfit{t}=\frac{\dot{\symbfit{r}}}{|\dot{\symbfit{r}}|}=\frac{\mathrm{d}\symbfit{r}}{\mathrm{d}s}=\symbfit{r}’$。用点号表示对非弧长参数求导，撇号表示对弧长参数$s$求导。
$$
\begin{align}
\dot{s}&=|\dot{\symbfit{r}}| \newline
\ddot{s}&=\frac{\dot{\symbfit{r}}\cdot \ddot{\symbfit{r}}}{|\dot{\symbfit{r}}|}\newline
t’&=\frac{1}{|\dot{\symbfit{r}}|}\newline
t’’&=-\frac{\dot{\symbfit{r}}\cdot\ddot{\symbfit{r}}}{\left(\dot{\symbfit{r}}\cdot\dot{\symbfit{r}}\right)^2}
\end{align}
$$

正则点：如果在曲线$\symbfit{r}(t)=[x(t), y(t), z(t)]^\mathrm{T}$上的点$P$处满足$\dot{\symbfit{r}}(t)\neq 0$；非正则点称为奇异点。

平面隐式曲线$f(x,y)=0$的单位切向量：$\symbfit{t}=\pm\frac{[f_y,\ -f_x]^{\mathrm{T}}}{\sqrt{f_x^2+f_y^2}}$。
空间隐式曲线定义为两个隐式曲面$f(x,y,z)=0$和$g(x,y,z)=0$的交线，曲线的单位切向量：$\symbfit{t}=\pm\frac{\nabla f\times\nabla g}{|\nabla f\times\nabla g|}$（在分母不为0时成立）。

主法向和曲率

对于曲线$\symbfit{r}$，$\symbfit{r}’(s)$是单位向量，$\symbfit{r}’\cdot\symbfit{r}’=1$，微分可得：$\symbfit{r}’\cdot\symbfit{r}’’=0$。则若$\symbfit{r}’’$非零向量，则垂直于单位切向量。
单位主法向：
$$
\symbfit{n}=\frac{\symbfit{r}’’(s)}{|\symbfit{r}’’(s)|}=\frac{\symbfit{t}’(s)}{|\symbfit{t}’(s)|}
$$
由单位切向量$\symbfit{t}$和单位法向量$\symbfit{n}$决定的平面称为在弧长$s$处的密切平面。

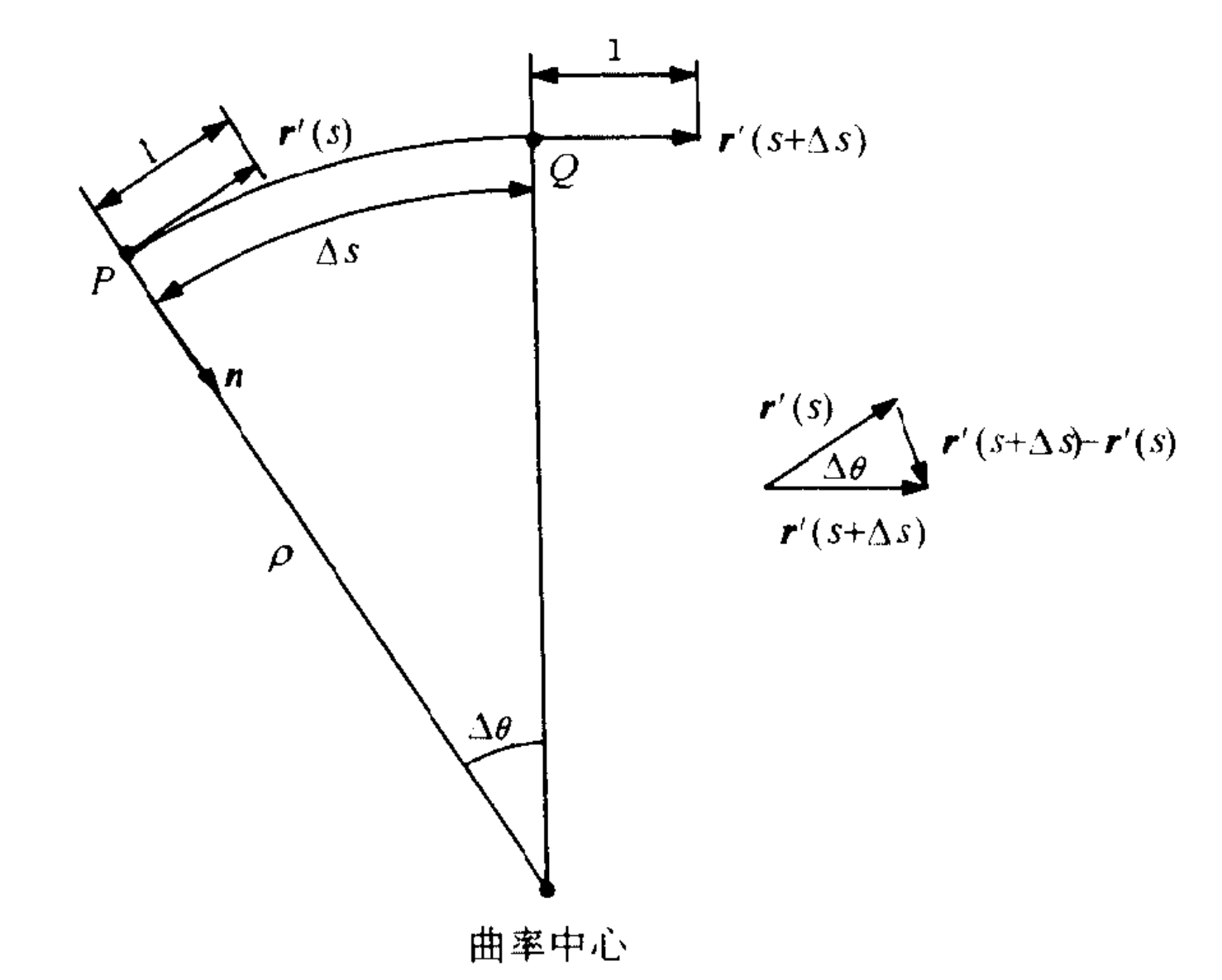
曲率与曲率半径：
$$
\kappa=\lim_{\Delta s\rightarrow 0} \frac{\Delta\theta}{\Delta s}=|\symbfit{r}’’(s)|=\frac{1}{\rho}
$$
曲率向量：$\symbfit{k}=\symbfit{r}’’=\symbfit{t}’=\kappa \symbfit{n}$表示切向量沿曲线的变化率。
拐点：曲线上曲率符号改变的点。

参数化平面曲线

单位法向量：$\symbfit{n}=\symbfit{e}_z\times\symbfit{t}=\frac{[-\dot{y},\ \dot{x}]^{\mathrm{T}}}{\sqrt{\dot{x}^2+\dot{y}^2}}$。
曲率：$\kappa=\frac{\dot{x}\ddot{y}-\ddot{x}\dot{y}}{\left(\dot{x}^2+\dot{y}^2\right)^{\frac32}}$。
隐式曲线：$\symbfit{n}=\frac{\nabla f}{|\nabla f|}$。

参数化空间曲线

曲率：$\kappa=\frac{|\dot{\symbfit{r}}\times\ddot{\symbfit{r}}|}{|\dot{\symbfit{r}}|^3}$。

隐式曲线：
$$
\begin{align}
\boldsymbol{\alpha}&=(\alpha_1,\alpha_2,\alpha_3)=\nabla f\times\nabla g \newline
\kappa&=\frac{\boldsymbol{\alpha}\times\left(\alpha_1\frac{\partial \boldsymbol{\alpha}}{\partial x}+\alpha_2\frac{\partial \boldsymbol{\alpha}}{\partial y}+\alpha_3\frac{\partial \boldsymbol{\alpha}}{\partial z}\right)}{|\boldsymbol{\alpha}|^3}
\end{align}
$$

副法向和挠率

副法向量：
$$
\begin{gather}
\symbfit{b}=\symbfit{t\times n}=\frac{\dot{\symbfit{r}}\times \ddot{\symbfit{r}}}{|\dot{\symbfit{r}}\times \ddot{\symbfit{r}}|}
\newline
\symbfit{b}’=\symbfit{t\times n’}
\end{gather}
$$

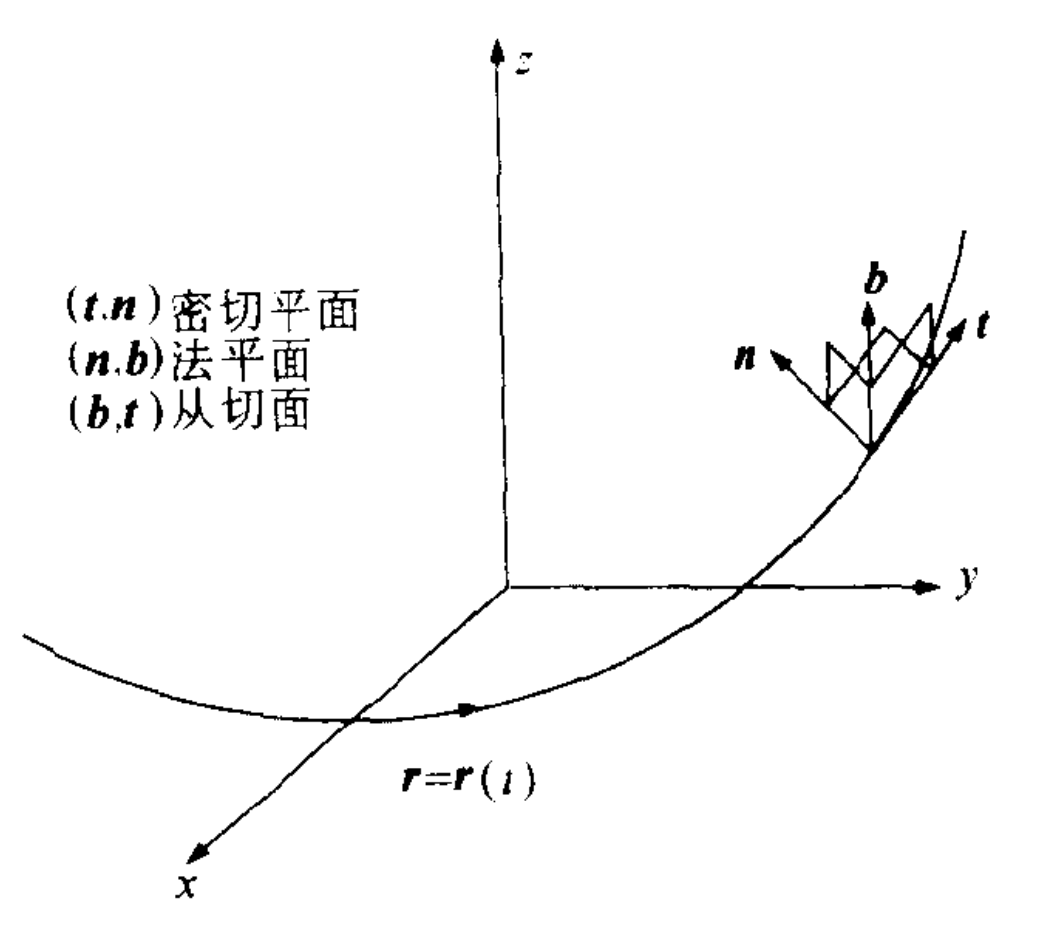
根据$\symbfit{n}$是单位向量，有：$\symbfit{n\cdot n}=1$，$\symbfit{n\cdot n’}=0$，$\symbfit{n}$垂直于从切平面$(\symbfit{b},\symbfit{t})$，所以$\symbfit{n’}$可以表示为如下线性组合：$\symbfit{n}’=\mu\symbfit{t}+\tau\symbfit{b}$。于是有：
$$
\symbfit{b}’=\tau\symbfit{t}\times\symbfit{b}=-\tau\symbfit{n}
$$
系数$\tau$称为挠率，是曲线与密切平面远离程度的度量。
$$
\tau=\frac{\symbfit{r}’\cdot (\symbfit{r’’\times r’’’})}{\symbfit{r’’\cdot r’’}}=\frac{(\symbfit{r’\ r’’\ r’’’})}{\symbfit{r’’\cdot r’’}}=\frac{(\dot{\symbfit{r}}\ \ddot{\symbfit{r}}\ \dddot{\symbfit{r}})}{(\dot{\symbfit{r}}\times\ddot{\symbfit{r}})\cdot(\dot{\symbfit{r}}\times\ddot{\symbfit{r}})}
$$
其中$(\symbfit{a\ b\ c})=(\symbfit{b\ c\ a})=(\symbfit{c\ a\ b})$表示三重数量积$\symbfit{a}\cdot(\symbfit{b\times c})$。
挠率既有大小又有负号。正挠率表示随弧长参数$s$增加，密切平面按照右手螺旋法则向切向$\symbfit{t}$方向旋转。如果挠率处处为0，则曲线为平面曲线。

Frenet-Serret公式

由上文可知：
$$
\begin{align}
\symbfit{t}’&=\kappa \symbfit{n} \newline
\symbfit{b}’&=-\tau\symbfit{n} \newline
\symbfit{n}’&=(\symbfit{b\times t})’=-\kappa\symbfit{t}+\tau\symbfit{b}
\end{align}
$$
可以将上述方程组表示为矩阵形式：
$$
\begin{bmatrix}
\symbfit{t}’ \newline \symbfit{n}’ \newline \symbfit{b}’
\end{bmatrix} = \begin{bmatrix}
0 & \kappa & 0 \newline
-\kappa & 0 & \tau \newline
0 & -\tau & 0
\end{bmatrix}\begin{bmatrix}
\symbfit{t} \newline \symbfit{n} \newline \symbfit{b}
\end{bmatrix}
$$
称为Frenet-Serret公式，描述了活动标架$(\symbfit{t}, \symbfit{n}, \symbfit{b})$沿曲线的运动。 对于任意速度曲线，对应公式为：
$$
\begin{bmatrix}
\dot{\symbfit{t}} \newline \dot{\symbfit{n}} \newline \dot{\symbfit{b}}
\end{bmatrix} = \begin{bmatrix}
0 & v\kappa & 0 \newline
-v\kappa & 0 & v\tau \newline
0 & -v\tau & 0
\end{bmatrix}\begin{bmatrix}
\symbfit{t} \newline \symbfit{n} \newline \symbfit{b}
\end{bmatrix}
$$
其中$v=\frac{\mathrm{d}s}{\mathrm{d}t}$为参数速度。