第3章 曲面的微分几何

切平面和曲面法向

考虑参数曲面$\symbfit{r}=\symbfit{r}(u,v)$的参数空间中一条曲线$u=u(t),v=v(t)$，则$\symbfit{r}=\symbfit{r}(t)=\symbfit{r}(u(t),v(t))$为参数曲面上一条参数曲线。曲面上曲线的切向量：
$$
\dot{\symbfit{r}}(t)=\frac{\partial \symbfit{r}}{\partial u}\dot{u}+\frac{\partial\symbfit{r}}{\partial v}\dot{v}=\symbfit{r}_u\dot{u}+\symbfit{r}_v\dot{v}
$$
点$P$处的切平面可以看作曲面上所有通过点$P$的曲线$\symbfit{r}(t)$的切向量的集合。
设$P$处参数记为$u_P,v_P$，在$\symbfit{r}(u_P,v_P)$处，切平面方程为：
$$
\symbfit{T}_P(\mu,\nu)=\symbfit{r}(u_P,v_P)+\mu\symbfit{r}_u(u_P,v_P)+\nu\symbfit{r}_v(u_P,v_P)
$$
单位法向量为：
$$
\symbfit{N}=\frac{\symbfit{r}_u\times\symbfit{r}_v}{|\symbfit{r}_u\times\symbfit{r}_v|}
$$
如果参数曲面上的点$P$处有$\symbfit{r}_u\times\symbfit{r}_v\neq \symbf{0}$，则称点$P$为正则点（普通点），否则为奇异点。

隐式曲面$f(x,y,z)=0$的单位法向量为：
$$
\symbfit{N}=\frac{\nabla f}{|\nabla f|}\quad (\nabla f\neq \symbf{0})
$$
在点$P(x_P,y_P,z_P)$处的切平面方程：
$$
f_x(x-x_P)+f_y(y-y_P)+f_z(z-z_P)=0
$$

第一基本齐式（度量）

考虑参数曲面上的曲线弧长微分：$\mathrm{d}s=|\symbfit{r}_u\dot{u}+\symbfit{r}_v\dot{v}|\mathrm{d}t=\sqrt{E\mathrm{d}u^2+2F\mathrm{d}u\mathrm{d}v+G\mathrm{d}v^2}$，其中
$$
E=\symbfit{r}_u\cdot\symbfit{r}_v\quad F=\symbfit{r}_u\cdot\symbfit{r}_v\quad G=\symbfit{r}_v\cdot\symbfit{r}_v
$$
第一基本齐式（first fundamental form）定义为
$$
\begin{align}
I=\mathrm{d}s^2=\mathrm{d}\symbfit{r}\cdot\mathrm{d}\symbfit{r}&=E\mathrm{d}u^2+2F\mathrm{d}u\mathrm{d}v+G\mathrm{d}v^2 \newline
&=\frac{(E\mathrm{d}u+F\mathrm{d}v)^2}{E}+\frac{EG-F^2}{E}\mathrm{d}v^2
\end{align}
$$
对于正则曲面：由于$EG-F^2=|\symbfit{r}_u\times\symbfit{r}_v|^2>0$和$E=|\symbfit{r}_u|>0$，所以$I$为正值。故$I\geqslant 0$，当且仅当$\mathrm{d}u=\mathrm{d}v=0$时，$I=0$。

参数曲面上两条曲线$\symbfit{r}_1=[u_1(t),\ v_1(t)]^{\mathrm{T}}$和$\symbfit{r}_2=[u_2(t),\ v_2(t)]^{\mathrm{T}}$之间的夹角可以通过内积来计算余弦值。两个切矢$\dot{\symbfit{r}}_1$和$\dot{\symbfit{r}}_2$互相垂直的条件为：
$$
E\mathrm{d}u_1\mathrm{d}u_2+F(\mathrm{d}u_1\mathrm{d}v_2+\mathrm{d}v_1\mathrm{d}u_2)+G\mathrm{d}v_1\mathrm{d}v_2=0
$$
特别当两条曲线为$u,v$等参数线时，有：
$$
\cos\omega=\frac{\symbfit{r}_u\cdot\symbfit{r}_v}{|\symbfit{r}_u||\symbfit{r}_v|}=\frac{F}{\sqrt{EG}}
$$
四个顶点$\boldsymbol{r}(u,v)$、$\boldsymbol{r}(u+\delta u,v)$、$\boldsymbol{r}(u,v+\delta v)$和$\boldsymbol{r}(u+\delta u,v+\delta v)$围成的小平行四边形的面积可以逼近为：$\delta A = \left| \boldsymbol{r}_u \delta u \times \boldsymbol{r}_v \delta v \right| = \sqrt{EG - F^2} \delta u \delta v$。微分形式为：
$$\mathrm{d}A = \sqrt{EG - F^2} , \mathrm{d}u\mathrm{d}v$$

第二基本齐式（曲率）

考虑曲面$S$上通过点$P$的一条曲线$C$，此处的单位切向量和单位法向量满足：$\symbfit{k} = \frac{\mathrm{d}t}{\mathrm{d}s} = \kappa \symbfit{n} = \symbfit{k}_{\mathrm{n}} + \symbfit{k}_{\mathrm{g}}$。其中$\symbfit{k}_{\mathrm{n}}=\kappa_{\mathrm{n}}\symbfit{N}$为法曲率向量，$\symbfit{k}_{\mathrm{g}}$为测地曲率向量。

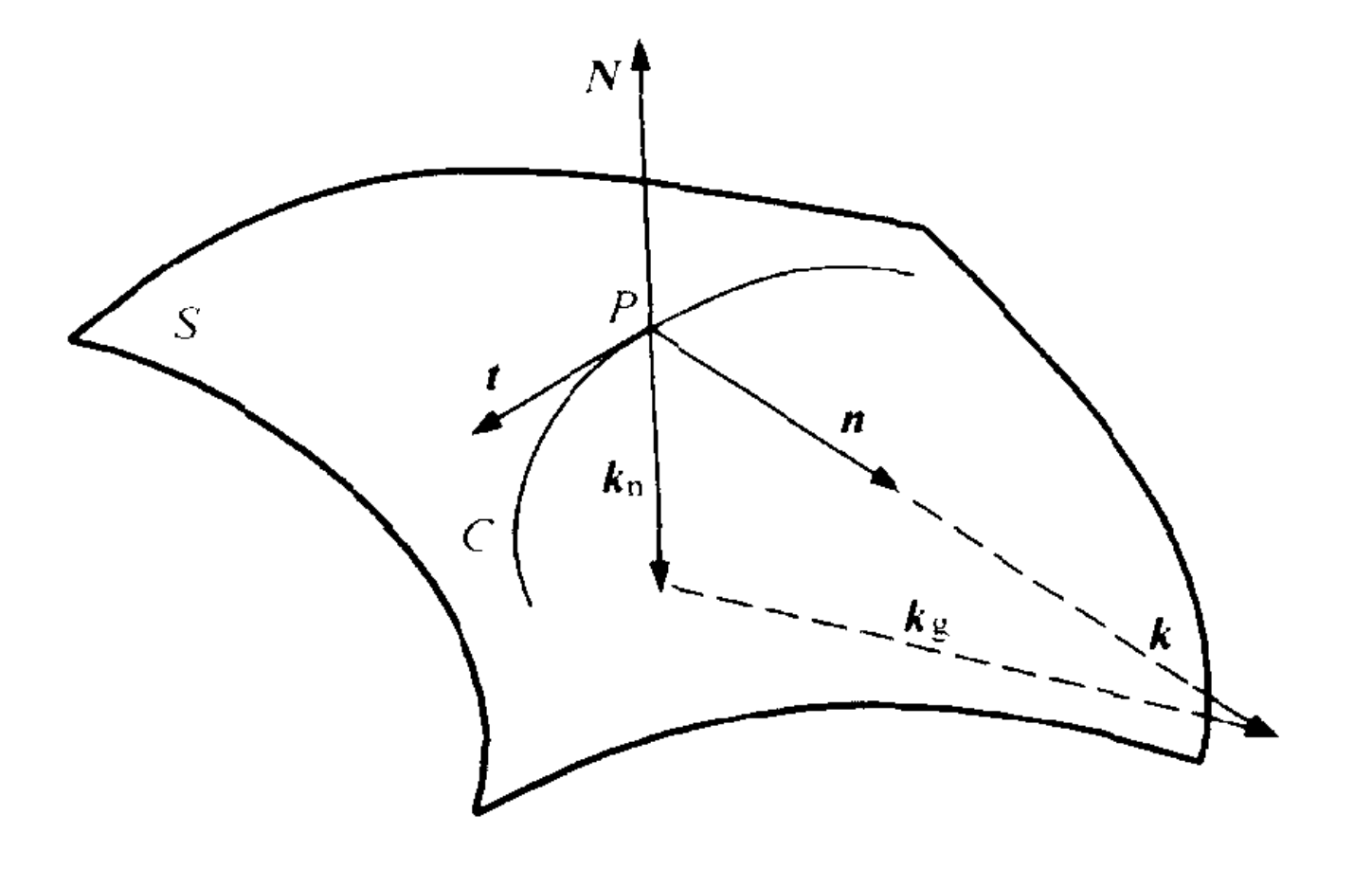
对于$\symbfit{N\cdot t}=0$沿曲线弧长微分可得：
$$\begin{align}
\kappa_{\mathrm{n}} &= \frac{\mathrm{d}\boldsymbol{t}}{\mathrm{d}s} \cdot \boldsymbol{N} = -\boldsymbol{t} \cdot \frac{\mathrm{d}\boldsymbol{N}}{\mathrm{d}s} = -\frac{\mathrm{d}\boldsymbol{r}}{\mathrm{d}s} \cdot \frac{\mathrm{d}\boldsymbol{N}}{\mathrm{d}s} = -\frac{\mathrm{d}\boldsymbol{r} \cdot \mathrm{d}\boldsymbol{N}}{\mathrm{d}\boldsymbol{r} \cdot \mathrm{d}\boldsymbol{r}} \newline
&= \frac{L\mathrm{d}u^2 + 2M\mathrm{d}u\mathrm{d}v + N\mathrm{d}v^2}{E\mathrm{d}u^2 + 2F\mathrm{d}u\mathrm{d}v + G\mathrm{d}v^2}
\end{align}$$
其中：
$$
\begin{align}
L &= - \boldsymbol{r}_u \cdot \boldsymbol{N}_u,\newline
M &= - \frac{1}{2} (\boldsymbol{r}_u \cdot \boldsymbol{N}_v + \boldsymbol{r}_v \cdot \boldsymbol{N}_u) = - \boldsymbol{r}_u \cdot \boldsymbol{N}_v = - \boldsymbol{r}_v \cdot \boldsymbol{N}_u \newline
N &= - \boldsymbol{r}_v \cdot \boldsymbol{N}_v
\end{align}$$
由于$\symbfit{r}_u$和$\symbfit{r}_v$都垂直于$\symbfit{N}$，可得：
$$L = \boldsymbol{r}_{uu} \cdot \boldsymbol{N}, \quad M = \boldsymbol{r}_{uv} \cdot \boldsymbol{N}, \quad N = \boldsymbol{r}_{vv} \cdot \boldsymbol{N}$$
第二基本齐式定义为：
$$
II=L\mathrm{d}u^2+2M\mathrm{d}u\mathrm{d}v+N\mathrm{d}v^2
$$
因此法曲率可以重写为：
$$
\kappa=\frac{II}{I}=\frac{L+2M\lambda+N\lambda^2}{E+2F\lambda+G\lambda^2}
$$
其中$\lambda=\frac{\mathrm{d}u}{\mathrm{d}v}$为曲线$C$在点$P$处的切线方向。由上可知法曲率只依赖于切向$\lambda$。
Meusnier定理：曲面$S$上过点$P$且具有相同切向的所有曲线在点$P$处具有相同的法曲率。
根据泰勒展开可得：
$$\begin{align}
\boldsymbol{PQ}&=\boldsymbol{r}(u + \mathrm{d}u, v + \mathrm{d}v)-\boldsymbol{r}(u, v)\newline
&=\boldsymbol{r}_u\mathrm{d}u+\boldsymbol{r}_v\mathrm{d}v+\frac{1}{2}(\boldsymbol{r}_{uu}\mathrm{d}u^2 + 2\boldsymbol{r}_{uv}\mathrm{d}u\mathrm{d}v+\boldsymbol{r}_{vv}\mathrm{d}v^2)+\cdots
\end{align}$$
忽略高阶项可得：
$$d = \boldsymbol{PQ} \cdot \boldsymbol{N} = (\boldsymbol{r}_u \mathrm{d}u + \boldsymbol{r}_v \mathrm{d}v) \cdot \boldsymbol{N} + \frac{1}{2} II=\frac{1}{2}II=\frac{1}{2}(L\mathrm{d}u^2+2M\mathrm{d}u\mathrm{d}v+N\mathrm{d}v^2)$$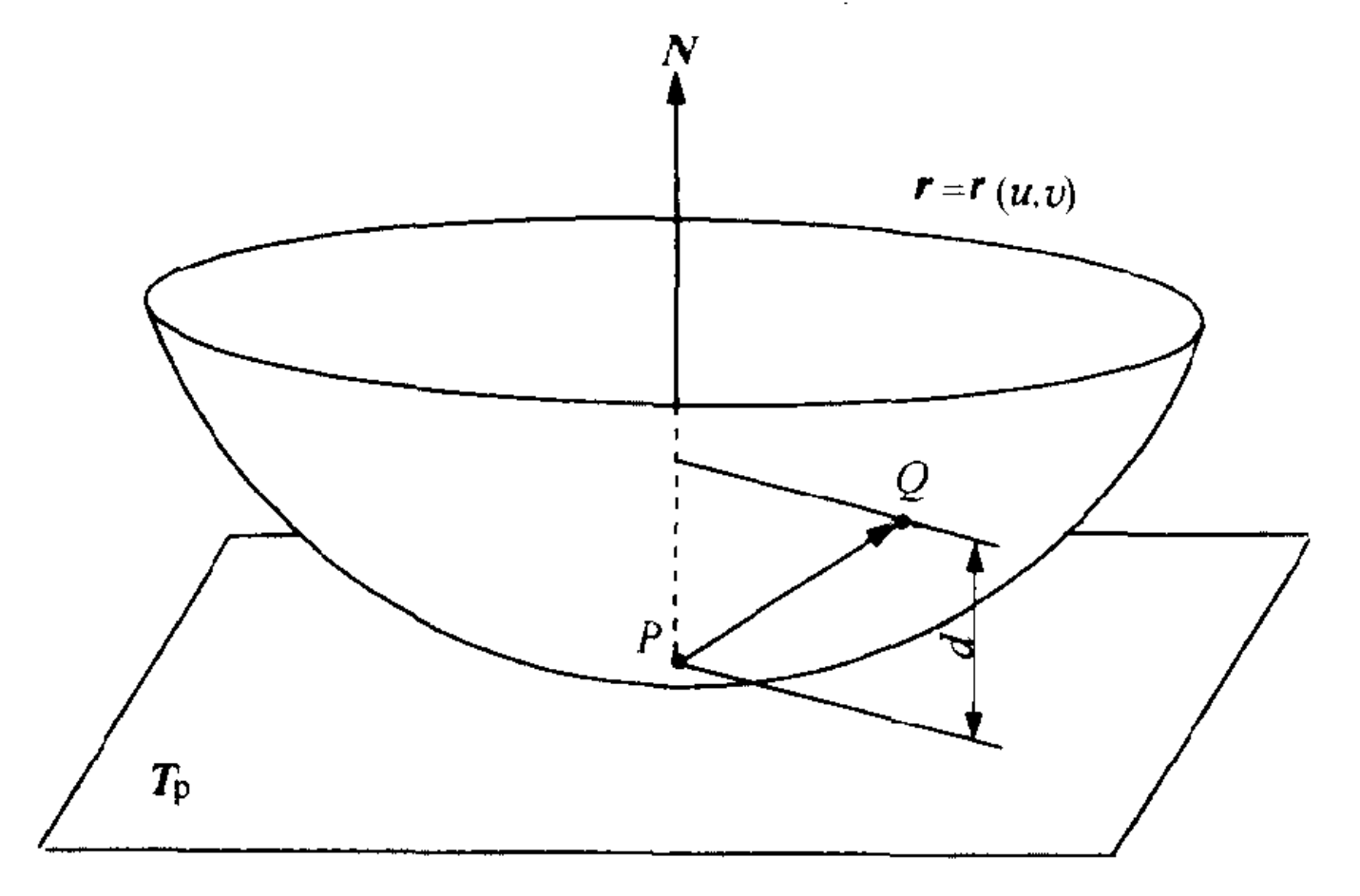

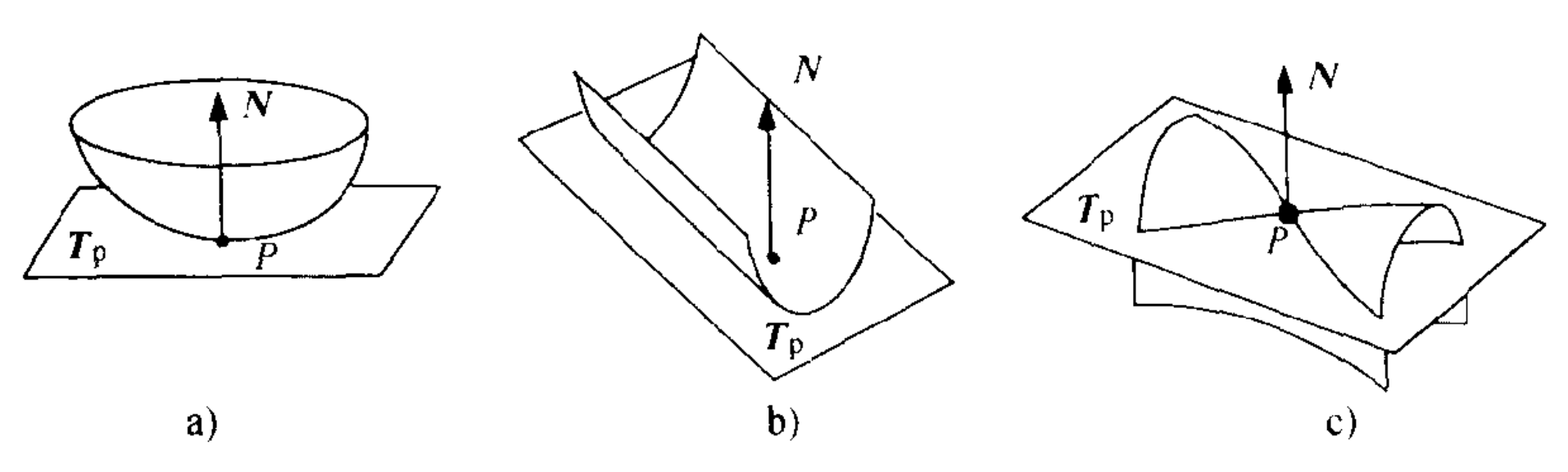
因此，$|II|$等于从点$Q$到点$P$处切平面的距离二阶逼近的两倍。当$d=0$时，公式变为$L\mathrm{d}u^{2}+2M\mathrm{d}u\mathrm{d}v + N\mathrm{d}v^{2} = 0$，假设$L\neq0$，可看作$\mathrm{d}u$的一元二次方程求解（若$L=0$且$N\neq 0$，求解$\mathrm{d}v$）。有如下四种情况：

• 当 $M^{2}-LN < 0$时，方程没有实根。这表明曲面与切平面仅交于点$P$，此时点 $P$称为椭圆点（如图 a 所示）。例如椭球面上均为椭圆点。
• 当$M^{2}-LN = 0$且$L^{2}+M^{2}+N^{2}\neq0$时，方程有重根。这表明曲面与切平面交于直线$\mathrm{d}u =-\frac{M}{L}\mathrm{d}v$，而直线通过点 $P$。此时点 $P$称为抛物点（如图 b 所示）。例如圆柱面上均为抛物点。
• 当$M^{2}-LN>0$时，方程有两个根。曲面与切平面在点$P$处交于两条直线$\mathrm{d}u=\frac{-M\pm\sqrt{M^{2}-LN}}{L}\mathrm{d}v$，这两条直线通过点 $P$。此时点 $P$称为双曲点（如图 c 所示）。例如旋转双曲面上均为双曲点。
• 当$L = M = N = 0$时，曲面与切平面在点$P$处具有高阶切触。此时点$P$ 称为平点（flat point）或平面点（planar point）。

主曲率

考虑法曲率$\kappa_{\mathrm{n}}$的极值（主曲率），令$\frac{\mathrm{d}\kappa_n}{\mathrm{d}\lambda} = 0$得到关于$\kappa_{\mathrm{n}}$的一元二次方程。当且仅当存在常数$k$使得：
$$
L=kE,\quad M=kF,\quad N=kG
$$
成立时（方程的判别式为0），该点称为脐点（umbilic）。该点处沿各个方向的法曲率是相同的。
定义：
$$
\begin{gather}
\text{高斯曲率}\quad K = \frac{LN - M^2}{EG - F^2}
\newline
\text{中曲率}\quad H = \frac{EN + GL - 2FM}{2(EG - F^2)}
\end{gather}
$$
则关于$\kappa_{\mathrm{n}}$的方程可以简化为$\kappa_{n}^{2}-2H\kappa_{n}+K = 0$，求解得到极值：
$$
\begin{gather}
\kappa_{\text{max}} = H + \sqrt{H^{2}-K} \newline
\kappa_{\text{min}} = H - \sqrt{H^{2}-K}
\end{gather}
$$
对应的主方向是：
$$\lambda = -\frac{M - \kappa_{\mathrm{n}} F}{N - \kappa_{\mathrm{n}} G} = -\frac{L - \kappa_{\mathrm{n}} E}{M - \kappa_{\mathrm{n}} F}$$
当$H^2=K$时，对应曲面上的脐点处，曲面局部等价于半径为$\frac{1}{|H|}$的球面。当$K=H=0$时，对应曲面上的平面点。
如果曲面上的一条曲线上所有点的切向均为该点的主曲率方向，那么该曲线称为曲率线。曲面的所有曲率线形成正交曲线网。
正交曲线网可以用于平面的参数化。参数线是曲率线的充要条件是：$F=M=0$。

高斯曲率和中曲率

高斯曲率和中曲率分别是了两个主曲率的乘积和平均：
$$
\begin{gather}
K=\kappa_{\max}\kappa_{\min} \newline
H=\frac{\kappa_{\max}+\kappa_{\min}}{2}
\end{gather}
$$
对于曲面上一点：

• $K>0$：椭圆点；
• $K<0$：双曲点；
• $K=0,H\neq 0$：抛物点；
• $K=H=0$：平面点。

显式曲面

曲面表示为显式形式$z=h(x,y)$时，可以写为参数形式$\symbfit{r}=\left[u\quad v\quad h(u,v)\right]^{\mathrm{T}}$，其中$u=x,v=y$。这种表示方法成为蒙日形式（Monger form），对应的曲面片称为蒙日曲面片。法向、第一和第二基本齐式的系数如下：
$$
\begin{gather}
E=1 + h_{x}^{2}, \quad F = h_{x}h_{y}, \quad G = 1 + h_{y}^{2}
\newline
\symbfit{N}=\frac{[-h_{x}\quad -h_{y}\quad 1]^{\mathrm{T}}}{\sqrt{1 + h_{x}^{2}+h_{y}^{2}}}
\newline
L=\frac{h_{xx}}{\sqrt{1 + h_{x}^{2}+h_{y}^{2}}}, \quad M=\frac{h_{xy}}{\sqrt{1 + h_{x}^{2}+h_{y}^{2}}}, \quad N=\frac{h_{yy}}{\sqrt{1 + h_{x}^{2}+h_{y}^{2}}}
\end{gather}
$$
故：
$$
\begin{gather}
K = \frac{LN - M^2}{EG - F^2} = \frac{h_{xx}h_{yy} - h_{xy}^2}{(1 + h_x^2 + h_y^2)^2} \newline
H = \frac{EN + GL - 2FM}{2(EG - F^2)} = \frac{(1 + h_x^2)h_{yy} - 2h_x h_y h_{xy} + (1 + h_y^2)h_{xx}}{2(1 + h_x^2 + h_y^2)^{\frac{3}{2}}}
\end{gather}
$$

隐式曲面

对于隐式曲面$f(x,y,z)=0$上的$f_z\neq 0$处，有$h_x=-\frac{f_x}{f_z}$，$h_y=-\frac{f_y}{f_z}$。二阶偏导数如下：
$$
\begin{gather}
h_{xx} = - \frac{\left( \frac{\partial f_x}{\partial x} \right)_y f_z - \left( \frac{\partial f_z}{\partial x} \right)_y f_x}{f_z^2} = \frac{2 f_x f_z f_{xz} - f_x^2 f_{zz} - f_z^2 f_{xx}}{f_z^3} \newline
h_{xy} = \frac{f_x f_z f_{yz} + f_y f_z f_{xz} - f_x f_y f_{zz} - f_z^2 f_{xy}}{f_z^3} \newline
h_{yy} = \frac{2f_y f_z f_{yz} - f_y^2 f_{zz} - f_z^2 f_{yy}}{f_z^3}
\end{gather}
$$
分别带入显式曲面对应式子即可得到第一和第二基本齐式的系数。如果$f_z=0$，可以通过对$x,y,z$的置换得到改变的公式。

二次曲面

可以通过适当的旋转消去交叉项，通过平移使得曲面以原点为中心以消去一阶项。二次曲面的中心定义为连接曲面上任意两点的一条弦的等分点。椭球面和双曲面具有中心，而抛物面没有中心。椭圆/双曲柱面是椭球面和双曲面的极限情形，椭圆锥面是单片和双片双曲面的渐近形式。于是二次曲面总可以表示为如下标准形式：
$$
f(x,y,z)=\zeta\frac{x^{2}}{a^{2}}+\eta\frac{y^{2}}{b^{2}}+\xi\frac{z^{2}}{c^{2}}-\delta = 0
$$
根据二次曲面的分类，$\zeta,\eta,\xi$可以取$-1,0$或$1$ ，$\delta$可以取$0$或$1$。

隐式二次曲面	$\zeta$	$\eta$	$\xi$	$\delta$	隐式二次曲面	$\zeta$	$\eta$	$\xi$	$\delta$
椭球面	$1$	$1$	$1$	$1$	椭圆柱面	$1$	$1$	$0$	$1$
单片双曲面	$1$	$1$	$-1$	$1$		$1$	$0$	$1$	$1$
	$1$	$-1$	$1$	$1$		$0$	$1$	$1$	$1$
	$-1$	$1$	$1$	$1$
双片双曲面	$1$	$-1$	$-1$	$1$	双曲柱面	$1$	$-1$	$0$	$1$
	$-1$	$1$	$-1$	$1$		$-1$	$1$	$0$	$1$
	$-1$	$-1$	$1$	$1$		$1$	$0$	$-1$	$1$
椭圆锥面	$1$	$1$	$-1$	$0$		$-1$	$0$	$1$	$1$
	$1$	$-1$	$1$	$0$		$0$	$1$	$-1$	$1$
	$-1$	$1$	$1$	$0$		$0$	$-1$	$1$	$1$

利用上述隐式曲面公式可得：
$$
\begin{gather}
K(x,y,z) = \frac{\zeta\eta\xi\delta}{a^{2}b^{2}c^{2}\left(\zeta^{2}\frac{x^{2}}{a^{4}}+\eta^{2}\frac{y^{2}}{b^{4}}+\xi^{2}\frac{z^{2}}{c^{4}}\right)^{2}} \newline
H(x,y,z) = -\frac{\zeta^{2}b^{2}c^{2}(\xi b^{2}+\eta c^{2})x^{2}+\eta^{2}a^{2}c^{2}(\xi a^{2}+\zeta c^{2})y^{2}+\xi^{2}a^{2}b^{2}(\eta a^{2}+\zeta b^{2})z^{2}}{2a^{4}b^{4}c^{4}\left(\zeta^{2}\frac{x^{2}}{a^{4}}+\eta^{2}\frac{y^{2}}{b^{4}}+\xi^{2}\frac{z^{2}}{c^{4}}\right)^{\frac{3}{2}}}
\end{gather}
$$
于是主曲率为$\kappa=H\pm\sqrt{H^2-K}$。

双曲柱面（$\zeta = \delta = 1$, $\eta = -1$, $\xi = 0$）$f(x,y)=\frac{x^2}{a^2}-\frac{y^2}{b^2}-1=0$的曲率为：
$$
\begin{gather}
K=0,\quad H=\frac{b^{2}x^{2}-a^{2}y^{2}}{2a^{4}b^{4}\left(\frac{x^{2}}{a^{4}}+\frac{y^{2}}{b^{4}}\right)^{\frac{3}{2}}}
\newline
\kappa_{\max} = \frac{b^{2}x^{2} - a^{2}y^{2}}{a^{4}b^{4}\left(\frac{x^{2}}{a^{4}} + \frac{y^{2}}{b^{4}}\right)^{\frac{3}{2}}}, \quad \kappa_{\min} = 0
\end{gather}$$
椭球面（$\zeta = \eta = \xi = \delta = 1$）$f(x,y,z)=\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}-1 = 0$的曲率为：
$$
\begin{gather}
K = \frac{1}{a^{2}b^{2}c^{2}\left(\frac{x^{2}}{a^{4}}+\frac{y^{2}}{b^{4}}+\frac{z^{2}}{c^{4}}\right)^{2}}, \quad H = \frac{x^{2}+y^{2}+z^{2}-a^{2}-b^{2}-c^{2}}{2a^{2}b^{2}c^{2}\left(\frac{x^{2}}{a^{4}}+\frac{y^{2}}{b^{4}}+\frac{z^{2}}{c^{4}}\right)^{\frac{3}{2}}} \newline
\kappa = \frac{x^{2}+y^{2}+z^{2}-a^{2}-b^{2}-c^{2}}{2a^{2}b^{2}c^{2}\left(\frac{x^{2}}{a^{4}}+\frac{y^{2}}{b^{4}}+\frac{z^{2}}{c^{4}}\right)^{\frac{3}{2}}}\pm\frac{\sqrt{(x^{2}+y^{2}+z^{2}-a^{2}-b^{2}-c^{2})^{2}-4a^{2}b^{2}c^{2}\left(\frac{x^{2}}{a^{4}}+\frac{y^{2}}{b^{4}}+\frac{z^{2}}{c^{4}}\right)}}{2a^{2}b^{2}c^{2}\left(\frac{x^{2}}{a^{4}}+\frac{y^{2}}{b^{4}}+\frac{z^{2}}{c^{4}}\right)^{\frac{3}{2}}}
\end{gather}
$$
特别地，对于半径为$R$的球面，可以得到：$K=\frac{1}{R^2}$，$H=\kappa=-\frac{1}{R}$。
椭圆锥面（$\zeta = \eta = 1, \xi = -1, \delta = 0$）$f(x,y,z)=\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}} = 0$的曲率为：
$$
\begin{gather}
K = 0, \quad H = -\frac{x^{2}+y^{2}+z^{2}}{2a^{2}b^{2}c^{2}\left(\frac{x^{2}}{a^{4}}+\frac{y^{2}}{b^{4}}+\frac{z^{2}}{c^{4}}\right)^{\frac{3}{2}}}\newline
\kappa_{\max}=0, \quad \kappa_{\min}=-\frac{x^{2}+y^{2}+z^{2}}{a^{2}b^{2}c^{2}\left(\frac{x^{2}}{a^{4}}+\frac{y^{2}}{b^{4}}+\frac{z^{2}}{c^{4}}\right)^{\frac{3}{2}}}
\end{gather}$$

欧拉定理和丢潘标形

欧拉定理：在曲面上任意一点$P$处，沿任意一个参数方向（在切平面内）的法曲率可以表示为点$P$两个主曲率的线性组合：
$$
\kappa_{\mathrm{n}}=\kappa_1\cos^2\varPhi+\kappa_2\sin^2\varPhi
$$
其中夹角$\varPhi$是任意参数方向与$\kappa_1$对应主方向之间的夹角。