第6章 交线的微分几何

引言

一般情况下，交线的切向等于两个曲面的法向叉积。当曲面法向平行时，不能使用叉积方法确定切向。这类交点成为相切交点。

进一步的曲线微分几何知识

设弧长参数化的交线为$x=x(s),y=y(s),z=z(s)$，向量形式为$\symbfit{r}=\symbfit{c}(s)$。
$$
\begin{gather}
\symbfit{c}’(s)=\symbfit{t} \newline
\symbfit{c}’’(s)=\symbfit{k}=\kappa \symbfit{n}
\end{gather}
$$
其中 $\symbfit{t}$ 是单位切向量，$\symbfit{k}$为表示切向量变化率的曲率向量。
$$\kappa^2 = \symbfit{k} \cdot \symbfit{k} = \symbfit{c}’’ \cdot \symbfit{c}’’ $$
继续求微分可以得到三阶导数$\symbfit{c}’’’(s)$：
$$\symbfit{c}’’’(s) = \kappa’ \symbfit{n} + \kappa \symbfit{n}’ $$
用 Frenet-Serret 公式中第二个方程代替$\symbfit{n}’$可得：
$$\symbfit{c}’’’(s) = - \kappa^2 \symbfit{t} + \kappa’ \symbfit{n} + \kappa \tau \symbfit{b} $$
由于$\symbfit{t}$、$\symbfit{n}$、$\symbfit{b}$三个向量形成一个右手直角坐标系，在曲率不为零的前提下，可得挠率公式如下：
$$\tau = \frac{\symbfit{b} \cdot \symbfit{c}’’’}{\kappa}$$
当$\kappa=0$时，不能使用$\symbfit{c}’’(s)=\symbfit{k}=\kappa \symbfit{n}$定义单位主法向量，要考虑曲线的高阶导数。如果$\kappa\equiv 0$，那么曲线为直线，此时Frenet标架没有定义。若$\kappa =0$只在孤立点处成立，且$\kappa ‘\neq0$，则：
$$
\symbfit{c}’’’(s)=\kappa’\symbfit{n}
$$
该公式定义了主法向量，其中$\kappa’$可以由公式$\kappa’^2=\symbfit{c}’’’\cdot \symbfit{c}’’’$得到。如果$\kappa=\kappa’=0$且$\kappa’’\neq 0$，需要继续求导，得到曲线的四阶导数：
$$
\symbfit{c}^{(4)}(s)=\kappa’’ \symbfit{n}
$$
其中$(\kappa’’)^{2} = \symbfit{c}^{(4)} \cdot \symbfit{c}^{(4)}$。对于一般情形$\kappa = \kappa’ = \cdots = \kappa^{(j - 1)} = 0$且$\kappa^{(j)} \neq 0$，则有：
$$\symbfit{c}^{(j + 2)}(s) = \kappa^{(j)} \symbfit{n} $$
其中$(\kappa^{(j)})^{2} = \symbfit{c}^{(j + 2)} \cdot \symbfit{c}^{(j + 2)}$。
零曲率点的挠率可以计算如下：如果$\kappa = 0$且$\kappa’\neq 0$，则需计算曲线$\symbfit{c}(s)$的四阶导数$\symbfit{c}^{(4)}(s)$：
$$\begin{align}
\symbfit{c}^{(4)}(s) &= - 3\kappa\kappa’\symbfit{t} + (\kappa’’ - \kappa\tau^{2} - \kappa^{3})\symbfit{n} + (2\kappa’\tau + \kappa\tau’)\symbfit{b} \newline
&=\kappa’’\symbfit{n} + 2\kappa’\tau\symbfit{b}
\end{align}$$
因此
$$\tau = \frac{\symbfit{b} \cdot \symbfit{c}^{(4)}}{2\kappa’}$$
类似地可以得到：
$$\begin{align*}
\symbfit{c}^{(5)}(s) &= (-4\kappa\kappa’’ - 3(\kappa’)^{2} + \kappa^{4} + \kappa^{2}\tau^{2})\symbfit{t} + (\kappa’’’- 6\kappa^{2}\kappa’ - 3\kappa’\tau^{2} - 3\kappa\tau\tau’)\symbfit{n} \newline
&+ (3\kappa’’\tau + 3\kappa’\tau’ - \kappa^{3}\tau - \kappa\tau^{3} + \kappa\tau’’)\symbfit{b}
\end{align*}$$
因此，如果$\kappa = \kappa’ = 0$且$\kappa’’ \neq 0$，则$\tau$为：
$$\tau = \frac{\symbfit{b} \cdot \symbfit{c}^{(5)}}{3\kappa’’}$$
一般地，如果$\kappa = \kappa’ = \cdots = \kappa^{(j - 1)} = 0$且$\kappa^{(j)} \neq 0$，则有：
$$\tau = \frac{\symbfit{b} \cdot \symbfit{c}^{(j + 3)}}{(j + 1)\kappa^{(j)}} $$

假设两个参数曲面分别为$\symbfit{r}=\symbfit{r}^A(u_A,v_A)$和$\symbfit{r}=\symbfit{r}^B(u_B.v_B)$，记两个隐式曲面分别为$f^A(x,y,z)=0$和$f^B(x,y,z)=0$。假设这些曲面都是正则的，即：
$$\symbfit{r}_{u_{A}}^{A} \times \symbfit{r}_{v_{A}}^{A} \neq 0, \quad \symbfit{r}_{u_{B}}^{B} \times \symbfit{r}_{v_{B}}^{B} \neq 0, \quad \nabla f^{A} \neq 0, \quad \nabla f^{B} \neq 0$$
参数曲面和隐式曲面的单位法向量计算方法见于第3章。
上文对交线的微分几何研究都是独立于两个相交曲面的。另一方面，交线也可以看作两个相交曲面上的曲线，例如$uv$参数平面中的曲线$u=u(s),v=v(s)$定义了参数曲面$\symbfit{r}(u,v)$上的一条曲线$\symbfit{r}=\symbfit{c}(s)=\symbfit{r}(u(s),v(s))$；而曲线$x=x(s),y=y(s),z=z(s)$与约束$f(x(s),y(s),z(s))=0$一起定义了隐式曲面$f(x,y,z)=0$上的一条曲线。应用链式法则，可得：
$$\begin{align}
\symbfit{c}’(s) &= \symbfit{r}_u u’ + \symbfit{r}_v v’ \newline
\symbfit{c}’’(s) &= \symbfit{r}_{uu} (u’)^2 + 2\symbfit{r}_{uv} u’ v’ + \symbfit{r}_{vv} (v’)^2 + \symbfit{r}_u u’’ + \symbfit{r}_v v’’ \newline
\symbfit{c}’’’(s) &= \symbfit{r}_{uuu} (u’)^3 + 3\symbfit{r}_{uuv} (u’)^2 v’ + 3\symbfit{r}_{uvv} u’ (v’)^2 + \symbfit{r}_{vvv} (v’)^3 \newline
&\quad + 3(\symbfit{r}_{uu} u’ u’’ + \symbfit{r}_{uv} (u’’ v’ + u’ v’’) + \symbfit{r}_{vv} v’ v’’) + \symbfit{r}_u u’’’ + \symbfit{r}_v v’’’
\end{align}$$
类似地：
$$\begin{align*}
\frac{\mathrm{d}f}{\mathrm{d}s} &= f_x x’ + f_y y’ + f_z z’ = 0 \newline
\frac{\mathrm{d}^2f}{\mathrm{d}s^2} &= f_{xx} (x’)^2 + f_{yy} (y’)^2 + f_{zz} (z’)^2 + 2 (f_{xy} x’y’ + f_{yz} y’z’ + f_{xz} x’z’) \newline
&\quad + f_x x’’ + f_y y’’ + f_z z’’ = 0 \newline
\frac{\mathrm{d}^3f}{\mathrm{d}s^3} &= f_{xxx} (x’)^3 + f_{yyy} (y’)^3 + f_{zzz} (z’)^3 + 3 [f_{xxy} (x’)^2 y’ + f_{xxz} (x’)^2 z’ \newline
&\quad + f_{xyy} x’ (y’)^2 + f_{yyz} (y’)^2 z’ + f_{xzz} x’ (z’)^2 + f_{yzz} y’ (z’)^2 + 2 f_{xyz} x’y’z’] \newline
&\quad + 3 [f_{xx} x’ x’’ + f_{yy} y’ y’’ + f_{zz} z’ z’’ + f_{xy} (x’’ y’ + x’ y’’) \newline
&\quad + f_{yz} (y’’ z’ + y’ z’’) + f_{xz} (x’’ z’ + x’ z’’)] + f_x x’’’ + f_y y’’’ + f_z z’’’ = 0
\end{align*}$$

横截交线

切线方向

横截交线的切向量位于两个曲面的切平面内，因此切向可以通过计算两个曲面法向的叉积得到。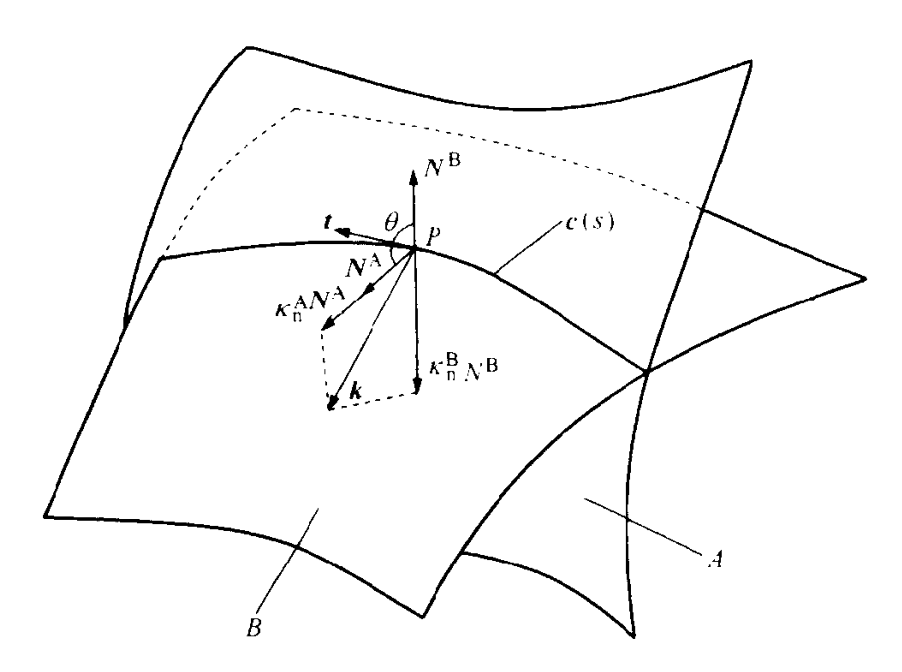

$$
\symbfit{t}=\frac{\symbfit{N}^A\times\symbfit{N}^B}{|\symbfit{N}^A\times\symbfit{N}^B|}
$$

曲率与曲率向量

交线上点$P$处的曲率向量垂直于切向，位于$\symbfit{N}^A$和$\symbfit{N}^B$所确定的法平面内。因此曲率向量可以表示为$\symbfit{k}=\alpha \symbfit{N}^A+\beta \symbfit{N}^B$。法曲率是曲率向量在单位曲面法向上的投影，$\kappa_{\mathrm{n}}=\symbfit{k}\cdot\symbfit{N}$。将曲率向量投影到两个曲面法向上，设$\theta$是$\symbfit{N}^A$和$\symbfit{N}^B$之间的夹角，$\cos\theta=\symbfit{N}^A\cdot\symbfit{N}^B$，可得：
$$\begin{gather}
\kappa_{\mathrm{n}}^{A} = \alpha + \beta \cos \theta \newline
\kappa_{\mathrm{n}}^{B} = \alpha \cos \theta + \beta
\end{gather}$$
求解方程组可得$\alpha,\beta$，可得：
$$\symbfit{k} = \frac{\kappa_\mathrm{n}^A - \kappa_\mathrm{n}^B \cos\theta}{\sin^2\theta} \symbfit{N}^A + \frac{\kappa_\mathrm{n}^B - \kappa_\mathrm{n}^A \cos\theta}{\sin^2\theta} \symbfit{N}^B$$
于是，只要计算出两个法曲率，就可以得到交线上点$P$处的曲率向量。
$E,F,G$为曲面第一基本齐式的系数，$L,M,N$为曲面第二基本齐式系数。
$$\begin{gather}
\kappa_{\mathrm{n}}=L(u’)^2+2Mu’v’+N(v’)^2 \newline
u’=\frac{(\symbfit{r}_u\cdot\symbfit{t})G-(\symbfit{r}_v\cdot\symbfit{t})F}{EG-F^2},\quad v’=\frac{(\symbfit{r}_v\cdot\symbfit{t})E-(\symbfit{r}_u\cdot\symbfit{t})F}{EG-F^2}
\end{gather}$$
对于隐式曲面，曲率向量$\symbfit{c}’’=(x’’,y’’,z’’)$在曲面的单位法向量$\frac{\nabla f}{|\nabla f|}$上的投影为：
$$\begin{align*}
\kappa_{\mathrm{n}} &= \frac{f_x x’’ + f_y y’’ + f_z z’’}{\sqrt{f_x^2 + f_y^2 + f_z^2}}\newline
&= -\frac{f_{xx}(x’)^2 + f_{yy}(y’)^2 + f_{zz}(z’)^2 + 2(f_{xy}x’y’ + f_{yz}y’z’ + f_{xz}x’z’)}{\sqrt{f_x^2 + f_y^2 + f_z^2}}
\end{align*}$$
交线$\symbfit{c}$在点$P$处的曲率为：
$$
\kappa = \sqrt{\symbfit{k}\cdot\symbfit{k}}=\frac{1}{|\sin\theta|}\sqrt{(\kappa_{\mathrm{n}}^A)^2+(\kappa_{\mathrm{n}}^B)^2+2\kappa_{\mathrm{n}}^A\kappa_{\mathrm{n}}^B\cos\theta}
$$

挠率和三阶导数向量

将$\symbfit{c}’’’(s)=-\kappa^2\symbfit{t}+\gamma\symbfit{N}^A+\delta\symbfit{N}^B$投影到曲面上点$P$处的单位法向量上，分量为：
$$\begin{gather}
\lambda_{\mathrm{n}}^A=\gamma+\delta\cos\theta\newline
\lambda_{\mathrm{n}}^B=\gamma\cos\theta+\delta
\end{gather}$$
求解可得$\gamma$和$\delta$，于是：
$$\symbfit{c}’’’ = -\kappa^2 \symbfit{t} + \frac{\lambda_{\mathrm{n}}^A - \lambda_{\mathrm{n}}^B \cos\theta}{\sin^2\theta} \symbfit{N}^A + \frac{\lambda_{\mathrm{n}}^B - \lambda_{\mathrm{n}}^A \cos\theta}{\sin^2\theta} \symbfit{N}^B$$
在计算$\symbfit{c}’’’$时需要知道$\lambda_{\mathrm{n}}^A$和$\lambda_{\mathrm{n}}^B$。对于参数曲面，$\lambda_{\mathrm{n}}$可以通过将$\symbfit{c}’’’$投影到曲面的单位法向量上得到：
$$\lambda_{\mathrm{n}} = \symbfit{c}’’’ \cdot \symbfit{N} = 3 \left[ Lu’u’’ + M(u’’v’ + u’v’’) + Nv’v’’ \right] + III $$
其中
$$III = \symbfit{r}_{uuu} \cdot \symbfit{N} (u’)^3 + 3\symbfit{r}_{uuv} \cdot \symbfit{N}(u’)^2 v’ + 3\symbfit{r}_{uvv} \cdot \symbfit{N} u’ (v’)^2 + \symbfit{r}_{vvv} \cdot \symbfit{N} (v’)^3$$
对于隐式曲面：
$$\lambda_{\mathrm{n}} = \frac{f_x x’’’ + f_y y’’’ + f_z z’’’}{\sqrt{f_x^2 + f_y^2 + f_z^2}} = -\frac{F_1 + F_2 + F_3}{\sqrt{f_x^2 + f_y^2 + f_z^2}}$$
其中
$$\begin{align}
F_1 &= f_{xxx}(x’)^3 + f_{yyy}(y’)^3 + f_{zzz}(z’)^3 \newline
F_2 &= 3[f_{xxy}(x’)^2 y’ + f_{x xz}(x’)^2 z’ + f_{xyy} x’(y’)^2 + f_{yyz} (y’)^2 z’ \newline
& \quad + f_{xzz} x’(z’)^2 + f_{yzz} y’(z’)^2 + 2f_{xyz} x’y’z’] \newline
F_3 &= 3[f_{xx} x’ x’’ + f_{yy} y’ y’’ + f_{zz} z’ z’’ + f_{xy} (x’’ y’ + x’ y’’) \newline
& \quad + f_{yz} (y’’ z’ + y’ z’’) + f_{xz} (x’’ z’ + x’ z’’)]
\end{align}$$
最后，挠率为：
$$
\tau = \frac{1}{\kappa \sin^2 \theta} \left\{ \left[ \lambda_{\mathrm{n}}^A - \lambda_{\mathrm{n}}^B \cos \theta \right] \left( \symbfit{b} \cdot \symbfit{N}^A \right) + \left[ \lambda_{\mathrm{n}}^B - \lambda_{\mathrm{n}}^A \cos \theta \right] \left( \symbfit{b} \cdot \symbfit{N}^B \right) \right\}
$$

更高阶导数向量

相切交点处的交线

假设曲面$A$和$B$在交线$\symbfit{c}(s)$上的点$P$处相切，即在点$P$处有$\symbfit{N}^A\parallel\symbfit{N}^B$。通过改变曲面的朝向，可以假设$\symbfit{N}^A=\symbfit{N}^B=\symbfit{N}$。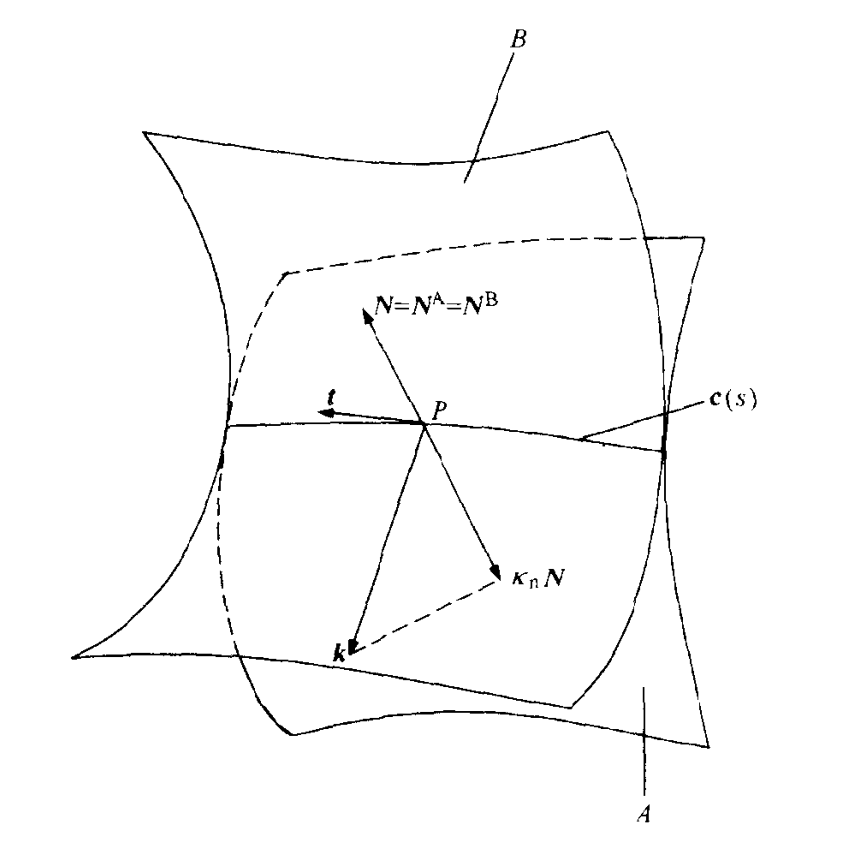

切线方向

曲线$\symbfit{c}(s)$在点$P$处的单位切向$\symbfit{t}$一定位于公共切平面内，因此$\symbfit{t}$可以表示为$\symbfit{r}_{u_A}^A$和$\symbfit{r}_{v_A}^A$或$\symbfit{r}_{u_B}^B$和$\symbfit{r}_{v_B}^B$ 的线性组合，即：
$$\symbfit{t} = \symbfit{r}_{u_A}^A u_A’ + \symbfit{r}_{v_A}^A v_A’ = \symbfit{r}_{u_B}^B u_B’ + \symbfit{r}_{v_B}^B v_B’$$
含有两个方程，四个未知量$u_A’,v_A’,u_B’,v_B’$。在点$P$处有$\symbfit{N}^A=\symbfit{N}^B=\symbfit{N}$，可得$\kappa_{\mathrm{n}}^A=\kappa_{\mathrm{n}}^B$，因此：
$$L^{A}\left(u_{A}’\right)^{2}+2 M^{A} u_{A}’v_{A}’+N^{A}\left(v_{A}’\right)^{2}=L^{B}\left(u_{B}’\right)^{2}+2 M^{B} u_{B}’ v_{B}’+N^{B}\left(v_{B}’\right)^{2}$$
再结合切向量的单位长度，形成一个具有四个变量、四个方程组成的非线性方程组。
求解时，$u’_{B}$和$v’_{B}$可以表示为$u’_{A}$和$v’_{A}$的线性组合：
$$\begin{gather}
u’_{B} = a_{11} u’_{A} + a_{12} v’_{A} \newline
v’_{B} = a_{21} u’_{A} + a_{22} v’_{A}
\end{gather}$$
其中
$$\begin{gather}
a_{11} = \frac{( \symbfit{r}_{u_{A}}^{A} \times \symbfit{r}_{v_{B}}^{B} ) \cdot \symbfit{N} }{( \symbfit{r}_{u_{B}}^{B} \times \symbfit{r}_{v_{B}}^{B} ) \cdot \symbfit{N} } = \frac{\det ( \symbfit{r}_{u_{A}}^{A}, \symbfit{r}_{v_{B}}^{B}, \symbfit{N} ) }{ \sqrt{E^{B} G^{B} - (F^{B})^2} } \newline
a_{12} = \frac{( \symbfit{r}_{v_{A}}^{A} \times \symbfit{r}_{v_{B}}^{B} ) \cdot \symbfit{N} }{( \symbfit{r}_{u_{B}}^{B} \times \symbfit{r}_{v_{B}}^{B} ) \cdot \symbfit{N} } = \frac{\det ( \symbfit{r}_{v_{A}}^{A}, \symbfit{r}_{v_{B}}^{B}, \symbfit{N} ) }{ \sqrt{E^{B} G^{B} - (F^{B})^2} } \newline
a_{21} = \frac{( \symbfit{r}_{u_{B}}^{B} \times \symbfit{r}_{u_{A}}^{A} ) \cdot \symbfit{N} }{( \symbfit{r}_{u_{B}}^{B} \times \symbfit{r}_{v_{B}}^{B} ) \cdot \symbfit{N} } = \frac{\det ( \symbfit{r}_{u_{B}}^{B}, \symbfit{r}_{u_{A}}^{A}, \symbfit{N} ) }{ \sqrt{E^{B} G^{B} - (F^{B})^2} } \newline
a_{22} = \frac{( \symbfit{r}_{u_{B}}^{B} \times \symbfit{r}_{v_{A}}^{A} ) \cdot \symbfit{N} }{( \symbfit{r}_{u_{B}}^{B} \times \symbfit{r}_{v_{B}}^{B} ) \cdot \symbfit{N} } = \frac{\det ( \symbfit{r}_{u_{B}}^{B}, \symbfit{r}_{v_{A}}^{A}, \symbfit{N} ) }{ \sqrt{E^{B} G^{B} - (F^{B})^2} }
\end{gather}$$
代入可得：
$$
b_{11}(u_A’)^2+2b_{12}u_A’v_A’+b_{22}(v_A’)^2=0 \tag{*}
$$
其中
$$\begin{align*}
b_{11}&=a_{11}^{2}L^{B} + 2a_{11}a_{21}M^{B} + a_{21}^{2}N^{B} - L^{A}\newline
b_{12}&=a_{11}a_{12}L^{B} + (a_{11}a_{22} + a_{21}a_{12})M^{B} + a_{21}a_{22}N^{B} - M^{A}\newline
b_{22}&=a_{12}^{2}L^{B} + 2a_{12}a_{22}M^{B} + a_{22}^{2}N^{B} - N^{A}
\end{align*}$$
当$b_{11}\neq 0$时，记$\omega=\frac{u_A’}{v_A’}$；或当$b_{11}=0$且$b_{22}\neq 0$时，记$\mu=\frac{v_A’}{u_A’}$，求解方程可以得到$\omega$或$\mu$，然后可以计算$\symbfit{t}$：
$$
\symbfit{t} = \frac{\omega \symbfit{r}_{u_{A}}^{A} + \symbfit{r}_{v_{A}}^{A}}{\left| \omega \symbfit{r}_{u_{A}}^{A} + \symbfit{r}_{v_{A}}^{A} \right|}\quad\text{或}\quad
\symbfit{t} = \frac{ \symbfit{r}_{u_{A}}^{A} + \mu\symbfit{r}_{v_{A}}^{A}}{\left| \symbfit{r}_{u_{A}}^{A} + \mu\symbfit{r}_{v_{A}}^{A} \right|}$$
根据判别式$b_{12}^2-b_{11}b_{22}$的值，方程的解分为四种情况：

1. 孤立相切交点：如果$b_{12}^2-b_{11}b_{22}<0$，那么方程没有实根。
2. 相切交线：如果$b_{12}^2-b_{11}b_{22}=0$且$b_{11}^2+b_{12}^2+b_{22}^2\neq 0$，那么方程有一个二重根，切向$\symbfit{t}$是唯一的。
3. 分支点：如果$b_{12}^2-b_{11}b_{22}>0$，那么方程有两个不同的根，存在交线$\symbfit{c}(s)$的另一个分支通过$P$。
4. 高阶切触点：如果$b_{11}=b_{12}=b_{22}=0$，那么对于任意$u_A’$和$v_A’$方程恒为0。此时曲面$A$和$B$在点$P$处至少具有二阶切触（曲率连续）。

当 $P$是一个曲面上的平点时，例如$\symbfit{r}^B$，那么 $L^B$、$M^B$、$N^B$ 均为零，此时方程仍可以计算。当 $P$是两个曲面上的平点时，两个曲面在点$P$ 处至少具有二阶接触，这属于上面讨论的情形 4。
根据二次方程的判别式，隐式-隐式和参数-隐式曲面之间的交线也有四种情形。

曲率和曲率向量

$$\begin{align*}
\symbfit{c}’’(s) &= \symbfit{r}_{u_A u_A}^A (u_A’)^2 + 2\symbfit{r}_{u_A v_A}^A u_A’ v_A’ + \symbfit{r}_{v_A v_A}^A (v_A’)^2 + \symbfit{r}_{u_A} u_A’’ + \symbfit{r}_{v_A} v_A’’ \newline
&= \symbfit{r}_{u_B u_B}^B (u_B’)^2 + 2\symbfit{r}_{u_B v_B}^B u_B’ v_B’ + \symbfit{r}_{v_B v_B}^B (v_B’)^2 + \symbfit{r}_{u_B} u_B’’ + \symbfit{r}_{v_B} v_B’’
\end{align*}$$
为了得到曲率向量 $\symbfit{k} = \symbfit{c}’’(s)$，需要确定系数 $(u’’_{A}, v’’_{A})$和$(u’’_{B}, v’’_{B})$。$(u_B’’,v_B’’)$可以表示为$(u_A’’,v_A’’)$的函数：
$$\begin{gather}
u’’_{B}=a_{11}u’’_{A}+a_{12}v’’_{A}+a_{13} \newline
v’’_{B}=a_{21}u’’_{A}+a_{22}v’’_{A}+a_{23}
\end{gather}$$
其中$a_{11},a_{12},a_{21},a_{22}$定义同上小节，$a_{13},a_{23}$定义如下：
$$\begin{gather}
\symbfit{\Lambda} = \symbfit{r}_{u_Bu_B}^{B}(u_B’)^2 + 2\symbfit{r}_{u_Bv_B}^{B}u_B’v_B’ + \symbfit{r}_{v_Bv_B}^{B}(v_B’)^2 - \symbfit{r}_{u_Au_A}^{A}(u_A’)^2 \newline
a_{13} = \frac{(\symbfit{\Lambda} \times \symbfit{r}_{v_{B}}^{B}) \cdot \symbfit{N}}{(\symbfit{r}_{u_{B}}^{B} \times \symbfit{r}_{v_{B}}^{B}) \cdot \symbfit{N}} = \frac{\det(\symbfit{\Lambda}, \symbfit{r}_{v_{B}}^{B}, \symbfit{N})}{\sqrt{E^{B} G^{B} - (F^{B})^2}} \newline
a_{23} = \frac{(\symbfit{r}_{u_{B}}^{B} \times \symbfit{\Lambda}) \cdot \symbfit{N}}{(\symbfit{r}_{u_{B}}^{B} \times \symbfit{r}_{v_{B}}^{B}) \cdot \symbfit{N}} = \frac{\det(\symbfit{r}_{u_{B}}^{B}, \symbfit{\Lambda}, \symbfit{N})}{\sqrt{E^{B} G^{B} - (F^{B})^2}}
\end{gather}$$
通过对交线$\symbfit{c}(s)=\symbfit{r}^A(u_A(s),v_A(s))=\symbfit{r}(u_B(s),v_B(s))$在点$P$处微分三次，将结果投影到法向量$\symbfit{N}$上，即条件$\lambda_{\mathrm{n}}^A=\lambda_{\mathrm{n}}^B$，可得额外一个方程：
$$\begin{align*}
&3\left[L^{A}u’_{A}u’’_{A} + M^{A}(u’’_{A}v’_{A}+u’_{A}v’’_{A})+N^{A}v’_{A}v’’_{A}\right]+III^{A}\newline
=&3\left[L^{B}u’_{B}u’’_{B} + M^{B}(u’’_{B}v’_{B}+u’_{B}v’’_{B})+N^{B}v’_{B}v’’_{B}\right]+III^{B}
\end{align*}$$
根据曲率向量$\symbfit{k}$垂直于切向量$\symbfit{t}$可得另外一个方程：
$$\symbfit{c}’’ \cdot \symbfit{t} = (\symbfit{r}_u \cdot \symbfit{t})u_A’’ + (\symbfit{r}_v \cdot \symbfit{t})v_A’’ + (\symbfit{r}_{uu} \cdot \symbfit{t})(u_A’)^2 + 2(\symbfit{r}_{uv} \cdot \symbfit{t})u_A’v_A’ + (\symbfit{r}_{vv} \cdot \symbfit{t})(v_A’)^2 = 0$$
求解得到$u_A’’$和$v_A’’$后，就可以得到曲率向量$\symbfit{k}$和曲率$\kappa$。
隐式-隐式和参数-隐式曲面间的交线的曲率都可以类似地得到。

三阶和更高阶导数向量

例子